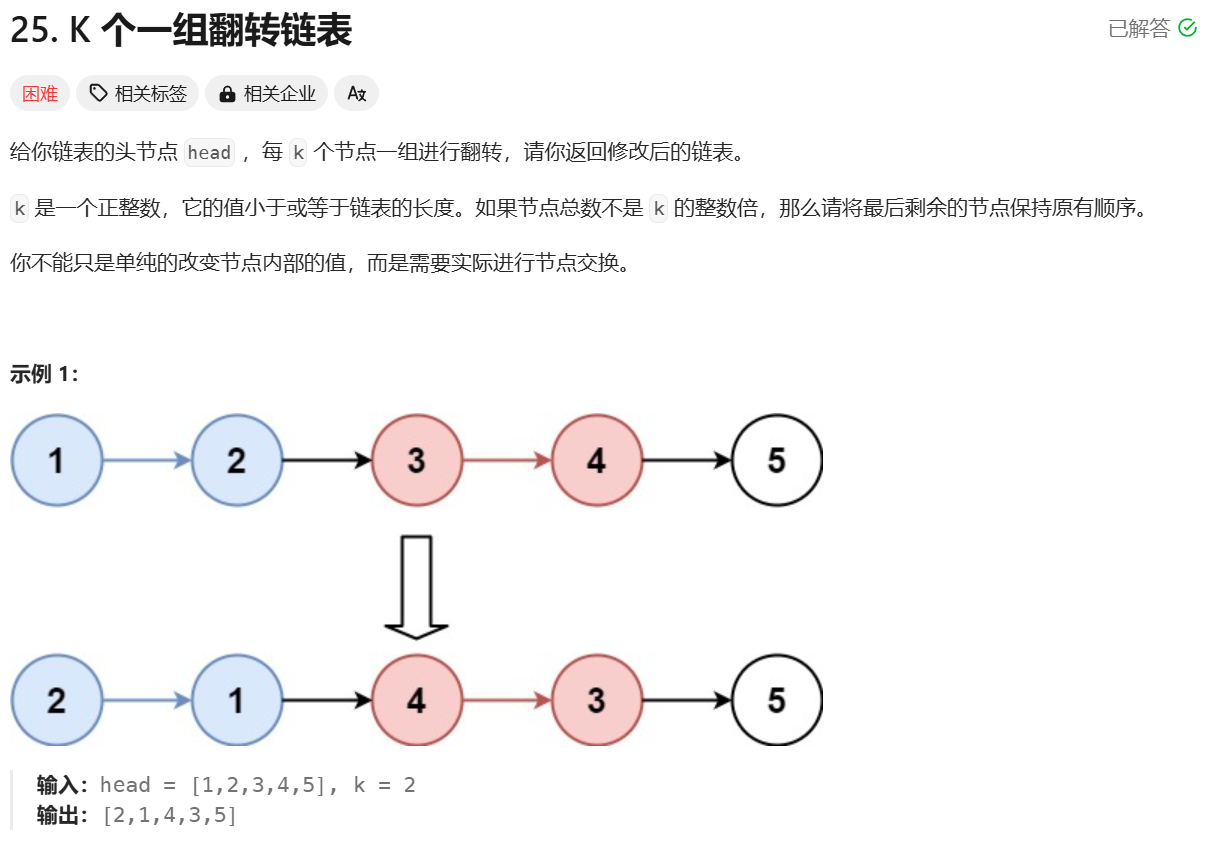
时间复杂度$O(log(m+n))$，要在两个排好序的数组中找到第k小的数

根据中位数的定义，当 m+n 是奇数时，中位数是两个有序数组中的第 (m+n)/2 + 1个元素，当 m+n 是偶数时，中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。

假设两个有序数组分别是 A 和 B。要找到第 k 小的元素，我们可以比较 A[k/2−1] 和 B[k/2−1]，其中 / 表示整数除法。由于 A[k/2−1] 和 B[k/2−1] 的前面分别有 A[0..k/2−2] 和 B[0..k/2−2]，即 k/2−1 个元素，对于 A[k/2−1] 和 B[k/2−1] 中的较小值，最多只会有 (k/2−1)+(k/2−1)≤k−2 个元素比它小，那么它就不能是第 k 小的数了。

因此我们可以归纳出三种情况：

如果 A[k/2−1]<B[k/2−1]，则比 A[k/2−1] 小的数最多只有 A 的前 k/2−1 个数和 B 的前 k/2−1 个数，即比 A[k/2−1] 小的数最多只有 k−2 个，因此 A[k/2−1] 不可能是第 k 个数，A[0] 到 A[k/2−1] 也都不可能是第 k 个数，可以全部排除。

如果 A[k/2−1]>B[k/2−1]，则可以排除 B[0] 到 B[k/2−1]。

如果相等，其实可以直接找到答案返回，也可以排除两段后继续递归

有以下三种情况需要特殊处理：

如果 A[k/2−1] 或者 B[k/2−1] 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 k 的值，而不能直接将 k 减去 k/2。

如果一个数组为空，说明该数组中的所有元素都被排除，我们可以直接返回另一个数组中第 k 小的元素。

如果 k=1，我们只要返回两个数组首元素的最小值即可。

class Solution {
public:   
int find(int k, const vector<int>& nums1, const vector<int>& nums2, int idx1, int idx2) { //找到第k小的数
	if (idx1 == nums1.size()) {
		return nums2[idx2 + k - 1];
	} else if (idx2 == nums2.size()) {
		return nums1[idx1 + k - 1];
	} else if (k == 1) {
		return min(nums1[idx1], nums2[idx2]);
	}
	int p = k / 2 - 1, x1 = 0, x2 = 0;
	if (p >= nums1.size() - idx1) {
		x1 = nums1[nums1.size() - 1];
		x2 = nums2[p + idx2];
		if (x1 > x2) {
			k -= (p + 1);
			idx2 = p + 1 + idx2;
		} else if (x1 < x2) {
			k -= (nums1.size() - idx1);
			idx1 = nums1.size();
		} else {
			k -= (p + 1);
			k -= (nums1.size() - idx1);
			idx2 = p + 1 + idx2;
			idx1 = nums1.size();
		}
	} else {
		if (p >= nums2.size() - idx2) {
			x1 = nums1[p + idx1];
			x2 = nums2[nums2.size() - 1];
			if (x1 > x2) {
				k -= (nums2.size() - idx2);
				idx2 = nums2.size();
		} else if (x1 < x2) {
				k -= (p + 1);
				idx1 = p + 1 + idx1;
		} else{
				k -= (p + 1);
				k -= (nums2.size() - idx2);
				idx1 = p + 1 + idx1;
				idx2 = nums2.size();
			}
		} else {
			x1 = nums1[p + idx1];
			x2 = nums2[p + idx2];
			if (x1 > x2) {
				k -= (p + 1);
				idx2 = p + 1 + idx2;
			} else if (x1 < x2) {
				k -= (p + 1);
				idx1 = p + 1 + idx1;
			} else {
				if (k % 2 == 0) {
					return x1;
				} else {
					return min(nums1[p + 1 + idx1], nums2[p + 1 + idx2]);
				}
			}
		}
	}
	return find(k, nums1, nums2, idx1, idx2);
}
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int l1 = nums1.size(), l2 = nums2.size();
        int sum = l1 + l2;
        double ans = 0;
        if(sum % 2 == 0){
            int k1 = sum / 2, k2 = k1 + 1;
            ans = (find(k1, nums1, nums2, 0, 0) + find(k2, nums1, nums2, 0, 0)) / 2.0;
        } else {
            int k = sum / 2 + 1;
            ans = find(k, nums1, nums2, 0, 0);
        }
        return ans;
    }
};